PID Control
PID Control
一、适用系统
二阶以内线性系统
二、控制系统概述
1. 开环控制系统
本质:没有眼睛的控制器。
控制器发出指令,系统照做,但不会根据实际结果修正。
优点:简单、快
缺点:不抗扰、不自适应
典型例子:微波炉按 30 秒就 30 秒,不会因为食物没热透自动再来一轮。
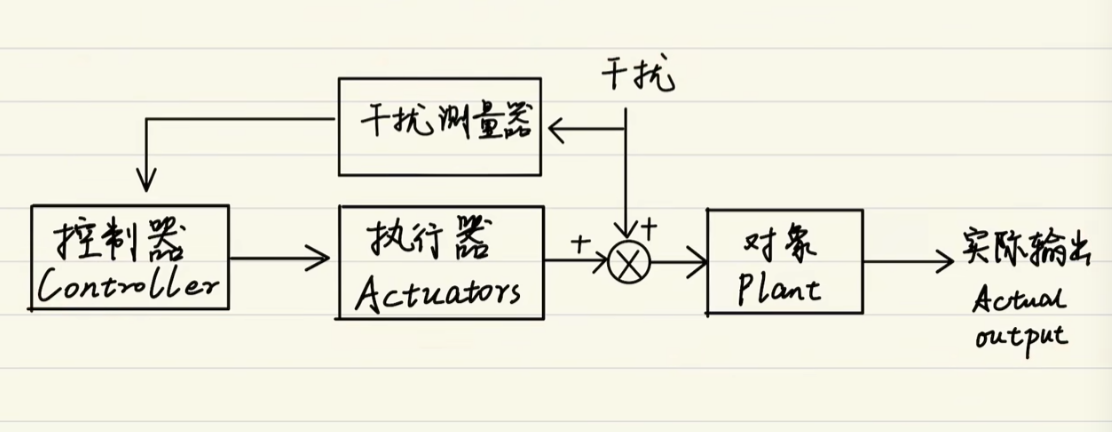
2. 前馈控制系统
本质:提前补偿扰动。
它根据已知模型,把扰动“抵消”掉,让输出不被影响。
优点:快、超前
缺点:模型错了就全错
常出现在机械臂、飞控里,比如提前补偿重力。
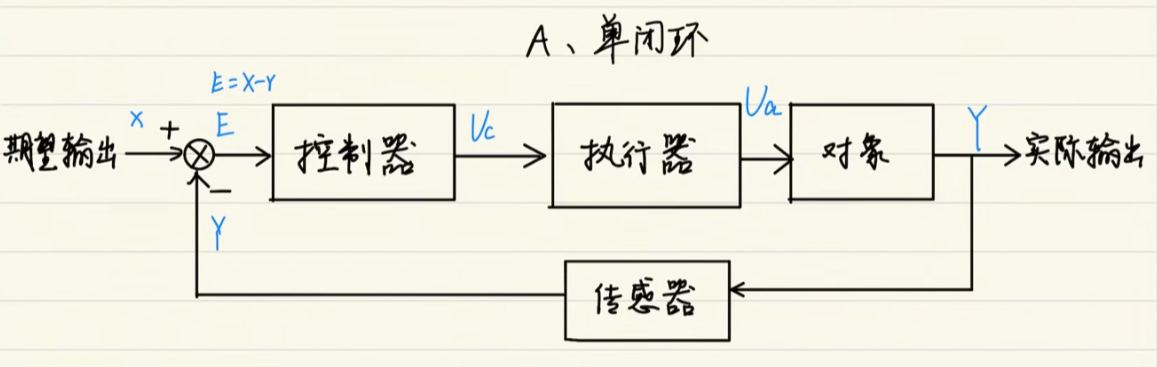
3. 单闭环控制系统
本质:系统终于安装了眼睛。
控制器根据误差修正指令,有抗扰能力。
缺点:慢于前馈,有滞后
优点:鲁棒、可靠
这是 PID 最经典的应用场景。
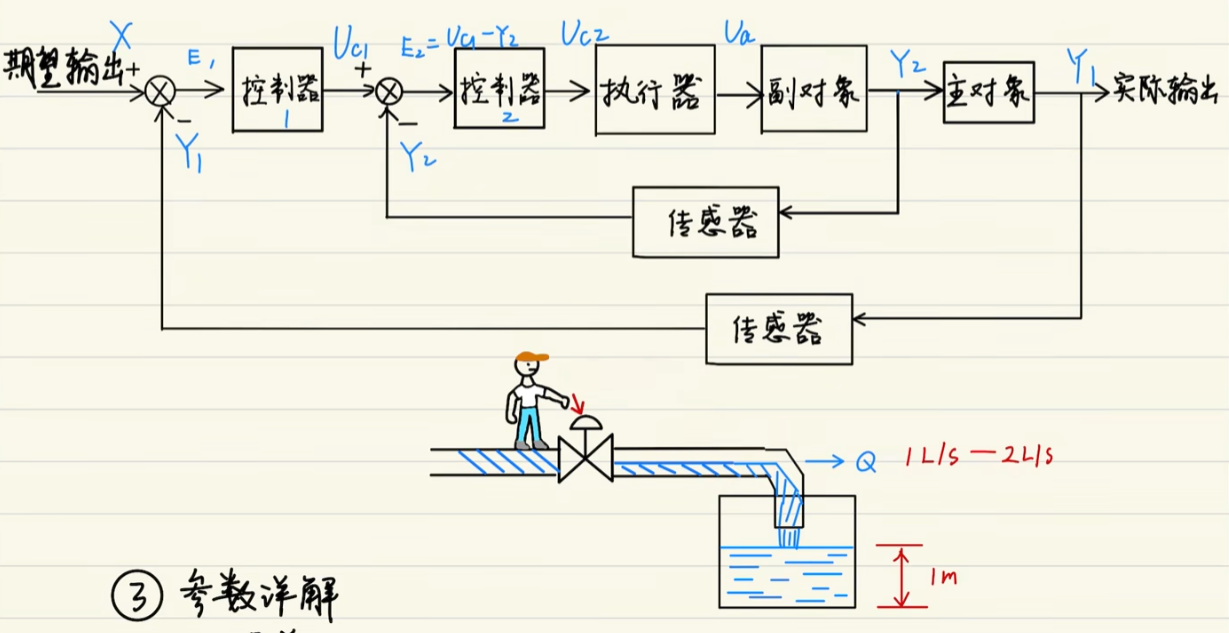
4. 双闭环控制系统
典型结构:外环调慢变量,内环调快变量。
比如伺服系统:位置环外 → 速度环内。
优势:提高整体动态性能
双环能让系统像“加了大脑和小脑”,一个掌方向,一个掌姿态。
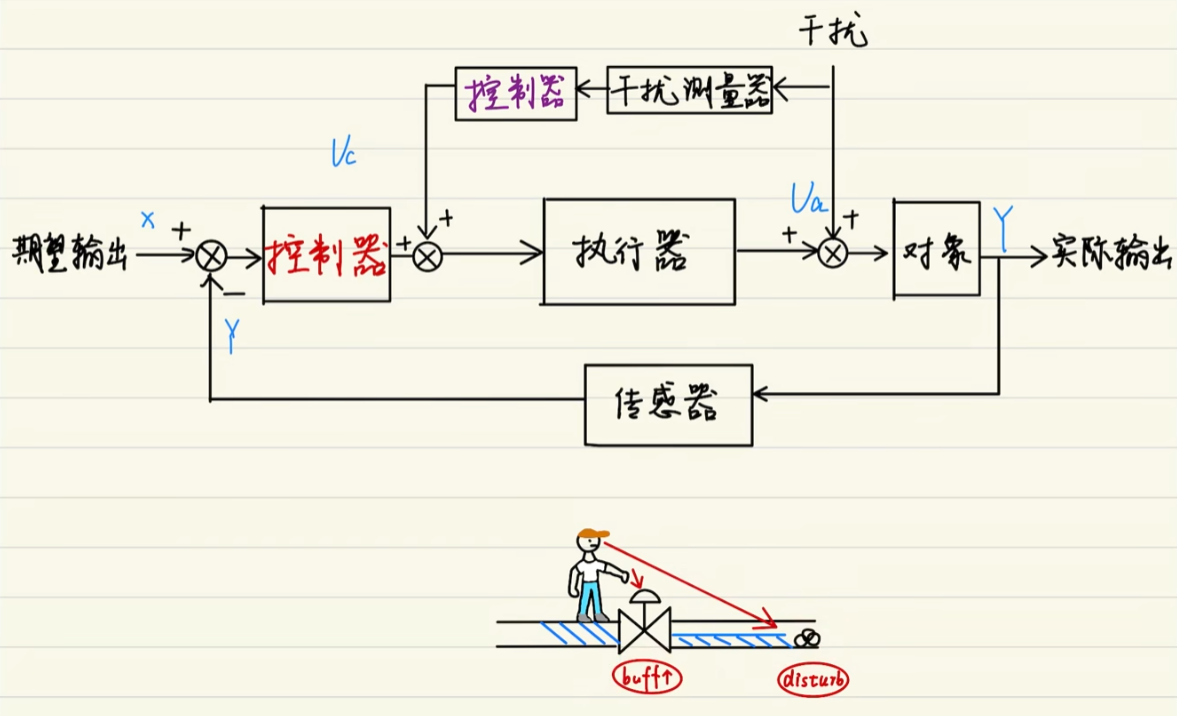
5. 前馈-反馈复合控制系统
喻为“预测 + 修正”双保险。
前馈负责提前补偿,反馈负责兜底。
在工业控制里非常常见,如电机抗负载扰动场景。
三、PID公式抽象
1. 定义:
$$
C = \frac{1}{P}\left( e + \frac{1}{T_i}\int_0^t e,dt + T_d \frac{de}{dt} \right)
$$
2. 连续:
$$
C = k_p e + k_i \int_0^t e,dt + k_d \frac{de}{dt}
$$
3. 离散:
$$
C = k_p e_i + k_i \sum_{i=1}^{N} e_i + k_d \frac{e_i - e_{i-1}}{\Delta t}
$$
进一步抽象:
$$
C = k_p e_i + k_i \sum_{i=1}^{N} e_i + k_d (e_i - e_{i-1})
$$
四、位置式&增量式
1. 位置式PID
位置式的思想是:
**每次计算输出的绝对值 $C_i$**,包含了全部历史贡献。
(1)工程表达:
$$
C_i = k_p e_i+ k_i \sum_{j=1}^{i} e_j+ k_d (e_i - e_{i-1})
$$
(2)特点
由于$Ii= \sum e_j$,历史误差全部累积,因此C 是绝对量:$C_i \quad \text{依赖于全部 } e_1, e_2, \dots, e_i$
所以:
- 容易积累大量积分 → 有饱和风险
- 执行器输出容易出现大跳变
- 工程中常需要加积分限幅
2. 增量式PID
增量式的思想是:
**不直接算输出,而是算输出的变化量 $\Delta C_i$**。
(1)工程表达:
$$
\Delta C(t) = C(t) - C(t - \Delta t)
$$
代入展开:
$$
\Delta C_i =k_p (e_i - e_{i-1})+ k_i e_i+ k_d (e_i - 2 e_{i-1} + e_{i-2})
$$
累加得到最终输出:
$$
C_i = C_{i-1} + \Delta C_i
$$
五、其余相关控制知识
1.积分限幅
问题来源:当执行机构饱和时,积分项还在疯狂增长,系统恢复后会“鬼畜式反弹”。
解决方法:对积分项做限制:
if (I > Imax) I = Imax;
if (I < Imin) I = Imin;
2. 积分分离
思想:误差大时,不让积分项掺和,免得越修越乱。
例如:
if (|err| < threshold) {
I += ki * err;
}
作用:避免大误差阶段的剧烈振荡
伺服定位系统最常见:大步跑用 P,小步走用 PI。
3. 微分先行
传统微分对误差求导:$D = k_d \frac{de}{dt}$
问题:误差的突变(如目标阶跃变化)会导致 D 项瞬间炸裂。
解决:改成对输出 y 微分而不是对误差微分:$D = -k_d \frac{dy}{dt}$
这让系统对目标阶跃更友好,减少一次“甩尾现象”。
4. 低通滤波的微分
微分对噪声极其敏感,所以常做成:
$D_i = \frac{N k_d}{1 + N \Delta t}
\left(
D_{i-1} + \Delta t (e_i - e_{i-1})
\right)$
类似于给 D 项加了 RC 滤波器,效果柔和很多。
5. 死区控制
为了避免小误差抖动,可以设置:
if (|err| < dz) output = 0;